目录
前言
这篇记录树的知识点以及PTA上考查树的题。
二叉树的定义
struct node{
int val;
node *lchild,*rchild;
}
二叉树的遍历
DFS遍历
先序遍历:
void Preorder(node *root){
if(root==NULL)return;
cout<<root->val<<' ';
Preorder(root->lchild);
Preorder(root->rchild);
}
中序遍历:
void Inorder(node *root){
if(root==NULL)return;
Inorder(root->lchild);
cout<<root->val<<' ';
Inorder(root->rchild);
}
后序遍历:
void Postorder(node *root){
if(root==NULL)return;
Postorder(root->lchild);
Postorder(root->rchild);
cout<<root->val<<' ';
}
BFS遍历
层序遍历:
void levelorder(node *root){
queue<node* >q;
q.push(root);
while(!q.empty()){
root=q.front();
q.pop();
cout<<root->val<<' ';
if(root->lchild!=NULL)q.push(root->lchild);
if(root->rchild!=NULL)q.push(root->rchild);
}
}
二叉树的建立
后序+中序建树+图解
PTA甲级:
A1020 Tree Traversals (25分)
Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, you are supposed to output the level order traversal sequence of the corresponding binary tree.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the postorder sequence and the third line gives the inorder sequence. All the numbers in a line are separated by a space.
Output Specification: For each test case, print in one line the level order traversal sequence of the corresponding binary tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
Sample Output:
4 1 6 3 5 7 2
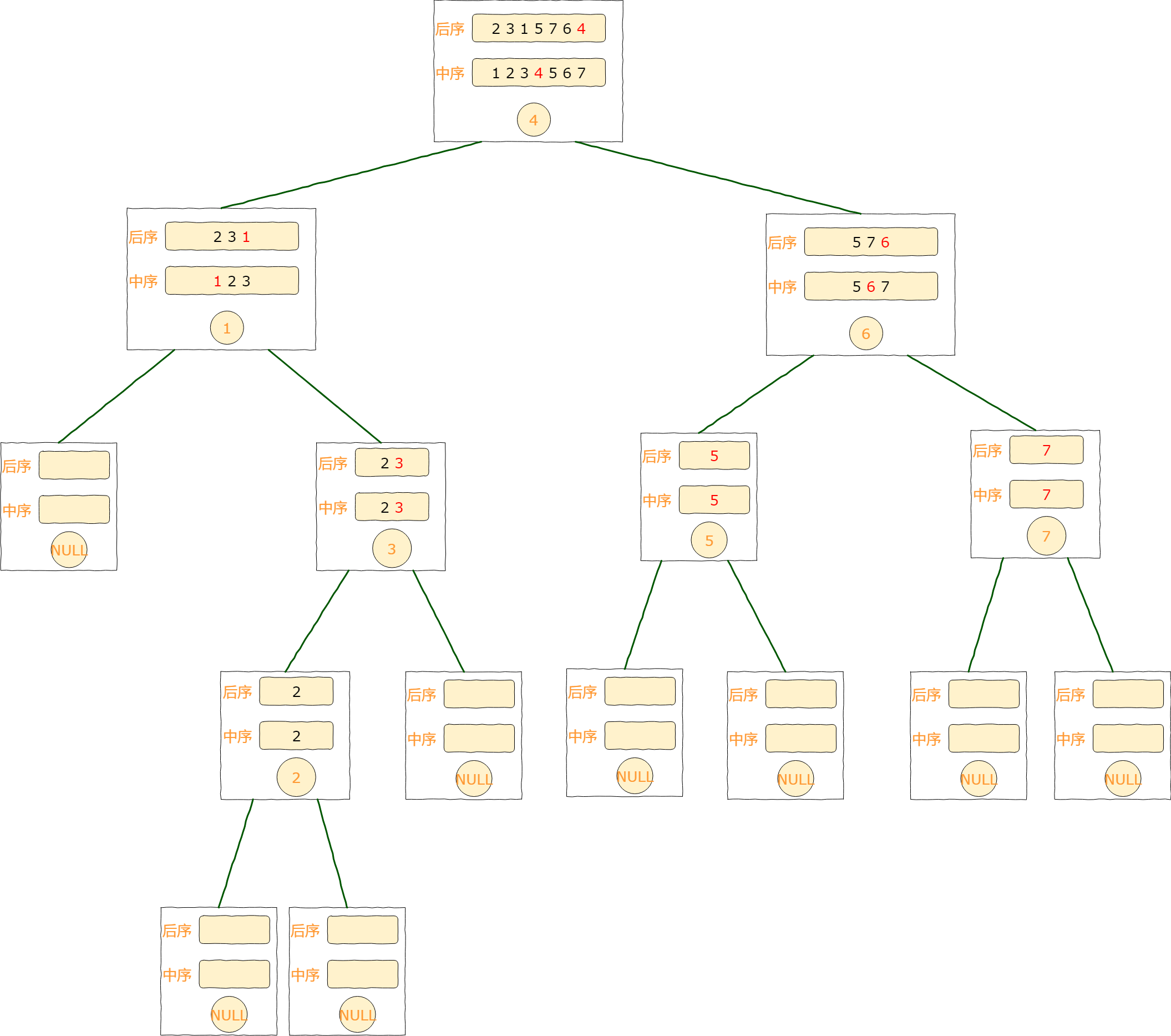
题目大意根据后序跟中序建树,最后按层序输出。
首先我们要知道:
1、在后序序列中,最后一个元素即为树的根节点。
2、然后在中序序列中找到根节结点元素所在的位置index,在这个index左边的序列为左子树的序列,在这个index右边的序列为右子树的序列
然后我们在递归时,每次找到当前位置的根节点即可创建一棵树。

#include<iostream>
#include<string>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<cstdio>
#include<algorithm>
using namespace std;
struct node{
node *Lchild,*Rchild;
int data;
};
int pre[55],in[55],post[55];
int n; //结点个数
node *create(int postL,int postR,int inL,int inR){
if(postL>postR){
return NULL; //后序序列长度小于等于0时,直接返回
}
node * root = new node; //创建一个新结点,用来存放当前二叉树的根结点
root->data = post[postR];//新结点的数据域为根节点的值
int k;
for(k=inL;k<=inR;k++){
if(in[k]==post[postR]){ //在中序序列中找到in[k]==pre[L]的结点
break;
}
}
int numLeft = k-inL; //左子树的结点个数
//返回左子树的根结点地址,赋值给root的左指针
root->Lchild=create(postL,postL+numLeft-1,inL,k-1);
root->Rchild=create(postL+numLeft,postR-1,k+1,inR);
return root;
}
int num =0; //已输出的结点个数
void BFS(node *root){ //层序输出
queue<node*>q;
node *now;
q.push(root);
while(!q.empty()){
now=q.front();
q.pop();
num++;
cout<<now->data;
if(num!=n)cout<<' ';
if(now->Lchild!=NULL) q.push(now->Lchild);
if(now->Rchild!=NULL) q.push(now->Rchild);
}
}
int main(){
cin>>n;
for(int i=0;i<n;i++)cin>>post[i];
for(int i=0;i<n;i++)cin>>in[i];
node *root = create(0,n-1,0,n-1);
BFS(root);
return 0;
}
先序+中序建树
L2-011 玩转二叉树 (25分)
给定一棵二叉树的中序遍历和前序遍历,请你先将树做个镜面反转,再输出反转后的层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例
7
1 2 3 4 5 6 7
4 1 3 2 6 5 7
输出样例:
4 6 1 7 5 3 2
根据先序跟中序建树,并将所有结点的左右子树交换,最后按层序输出。
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
struct node{
node *lchild,*rchild;
int data;
};
int n,num=0;
int pre[35],in[35];
node *create(int prel,int prer,int inl,int inr){
if(prel>prer)return NULL;
node *root=new node;
root->data=pre[prel];
int k;
for(k=inl;k<=inr;k++){
if(in[k]==pre[prel])break;
}
int numleft=k-inl;
root->lchild=create(prel+1,prel+numleft,inl,k-1);
root->rchild=create(prel+numleft+1,prer,k+1,inr);
return root;
}
void BFS(node *root){
node *now=root;
queue<node*>q;
q.push(now);
while(!q.empty()){
now=q.front();
q.pop();
cout<<now->data;
num++;if(num!=n)cout<<' ';
if(now->lchild!=NULL) q.push(now->lchild);
if(now->rchild!=NULL) q.push(now->rchild);
}
}
int main(){
cin>>n;
for(int i=0;i<n;i++)cin>>in[i];
for(int i=0;i<n;i++)cin>>pre[i];
node *root=create(0,n-1,0,n-1);//根据先序跟中序创建树
queue<node*>q; //利用队列实现左右子树的交换
q.push(root); //根节点入队
while(!q.empty()){ //当队列不为空
node *p=q.front(); //取队首
node *temp=p->lchild; //临时指针指向左孩子
p->lchild=p->rchild; //p的右孩子变成p的左孩子
p->rchild=temp; //p的左孩子变成p的右孩子
q.pop(); //出队
if(p->lchild!=NULL) q.push(p->lchild); //左孩子不为空则入队
if(p->rchild!=NULL) q.push(p->rchild);右孩子不为空则入队
}
BFS(root);
return 0;
}
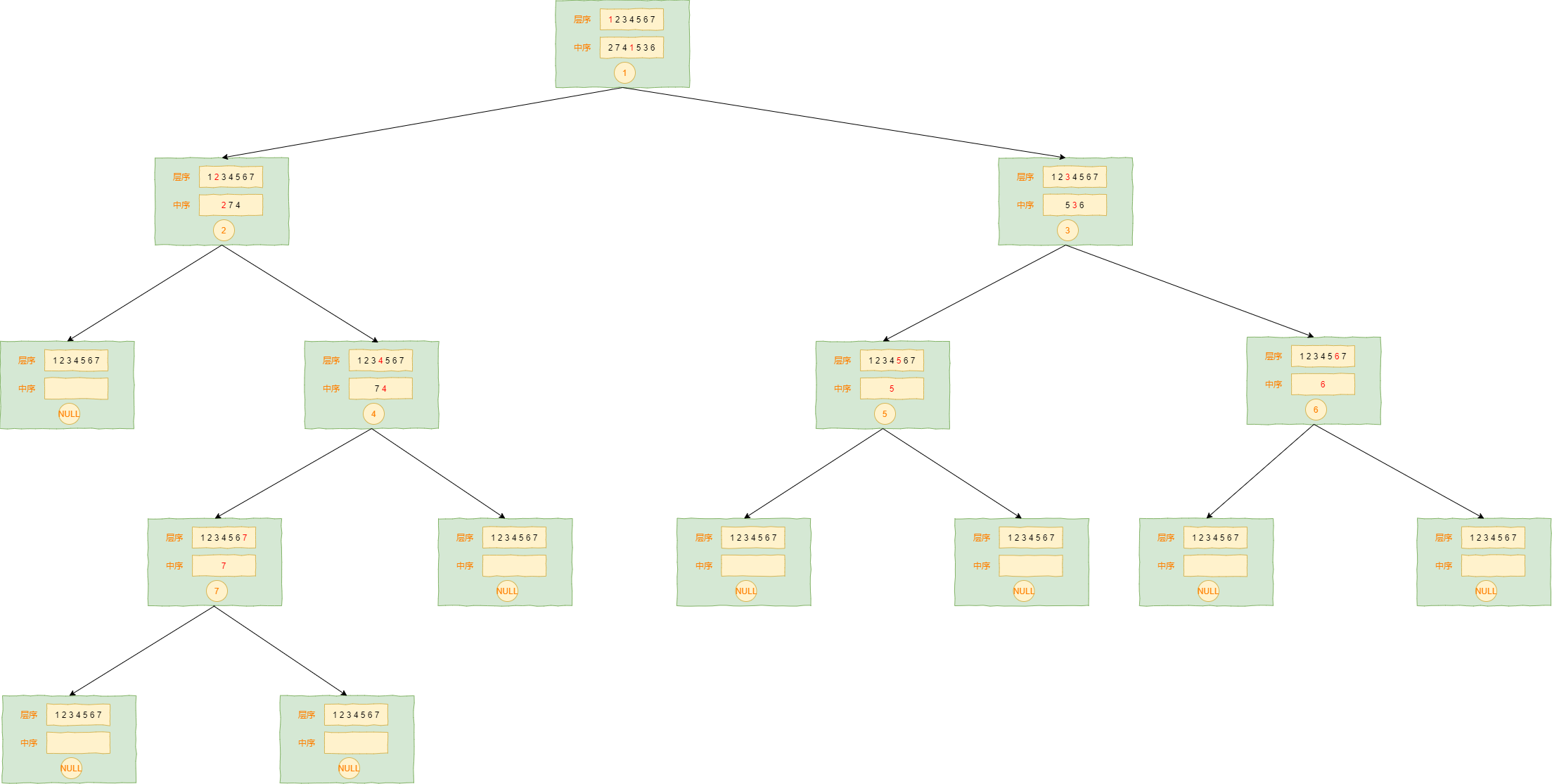
层序+中序建树图解
层序+中序建树与先序+中序建树的思路差不多,都是中序序列划分左右子树,先序或层序提供当前树的根节点。
首先要清楚:
1、层序的第一个结点即为当前树的根节点,所以每次55
2、已知当前树的根节点在中序序列中即可划分左右子树
 层序+中序建树图解
层序+中序建树图解
输入:
7
2 7 4 1 5 3 6
1 2 3 4 5 6 7
输出:
2 7 4 1 5 3 6
#include<bits/stdc++.h>
using namespace std;
struct node{
int val;
node *left,*right;
};
const int MAXN=1005;
int In[MAXN],Lv[MAXN],n;
int Find(int inL,int inR){ //找到当前中序序列中第一次在层序序列中出现的元素的下标
for(int i=0;i<n;i++){ //遍历层序序列
for(int j=inL;j<=inR;j++){ //遍历传入的中序子序列
if(Lv[i]==In[j]){
return i; //返回下标
}
}
}
}
//inL跟inR分别是中序序列中的左右边界,pos是从层序序列中找到根节点的下标
node *create(int inL,int inR,int pos){
if(inL>inR)return NULL;
node *root=new node;
root->val=Lv[pos]; //pos即为当前树的根节点元素
int i=inL;
for(;i<=inR;i++){ // 找到中序序列中根节点的下标
if(In[i]==Lv[pos])
break;
}
int num=i-inL; //获取左右子树的分界
root->left=create(inL,inL+num-1,Find(inL,inL+num-1)); //往左孩子递归建树
root->right=create(inL+num+1,inR,Find(inL+num+1,inR)); //往右孩子递归建树
return root; //返回当前的结点
}
void dfs(node *root){ //中序遍历
if(root==NULL)return;
dfs(root->left);
cout<<root->val<<' ';
dfs(root->right);
}
int main(){
cin>>n;
for(int i=0;i<n;i++)cin>>In[i]; //中序序列
for(int i=0;i<n;i++)cin>>Lv[i]; //层序序列
node *root=create(0,n-1,0); //建树
dfs(root); //打印
}
二叉搜索树的创建
#include<bits/stdc++.h>
using namespace std;
struct node{
int val;
node *lchild,*rchild;
};
node *insert(node *root,int val){
if(root==NULL){ //当结点为空时创建
root=new node;
root->val=val;
root->lchild=root->rchild=NULL;
}
else if(val<root->val) //当新插入的值比该结点值小则去左子树创建
root->lchild=insert(root->lchild,val);
else
root->rchild=insert(root->rchild,val); //当新插入的值大或等于该结点值则去右子树创建
}
void Preorder(node *root){
if(root==NULL)return;
cout<<root->val<<' ';
Preorder(root->lchild);
Preorder(root->rchild);
}
void Inorder(node *root){
if(root==NULL)return;
Inorder(root->lchild);
cout<<root->val<<' ';
Inorder(root->rchild);
}
void Postorder(node *root){
if(root==NULL)return;
Postorder(root->lchild);
Postorder(root->rchild);
cout<<root->val<<' ';
}
void levelorder(node *root){
queue<node* >q;
q.push(root);
while(!q.empty()){
root=q.front();
q.pop();
cout<<root->val<<' ';
if(root->lchild!=NULL)q.push(root->lchild);
if(root->rchild!=NULL)q.push(root->rchild);
}
}
int main(){
int N,val;
cin>>N;
node *root=NULL;
for(int i=0;i<N;i++){
cin>>val;
root=insert(root,val);
}
cout<<"先序遍历:";
Preorder(root);
cout<<"\n中序遍历:";
Inorder(root);
cout<<"\n后序遍历:";
Postorder(root);
cout<<"\n层序遍历:";
levelorder(root);
return 0;
}
平衡二叉树的创建+旋转图解
平衡二叉树失衡的类型有RR、LL、RL、LR四种类型。
当失衡的类型为RR时,只进行左旋,当失衡类型为LL时,只进行右旋。
当失衡的类型为RL时,先对失衡结点的右孩子进行右旋,再对该失衡结点进行左旋。
当失衡的类型为LR时,先对失衡结点的左孩子进行左旋,再对该失衡结点进行右旋。
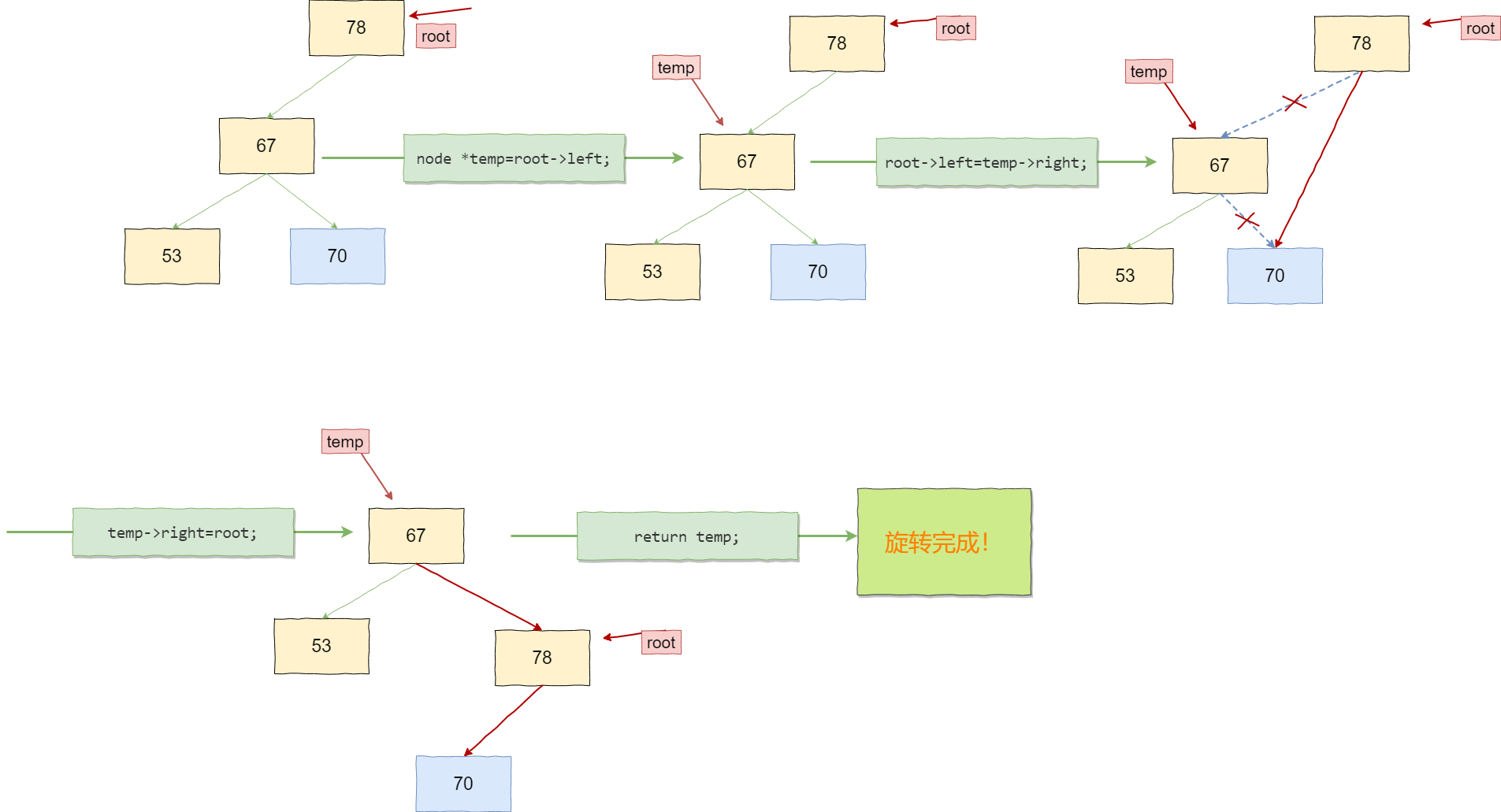 右单旋
右单旋
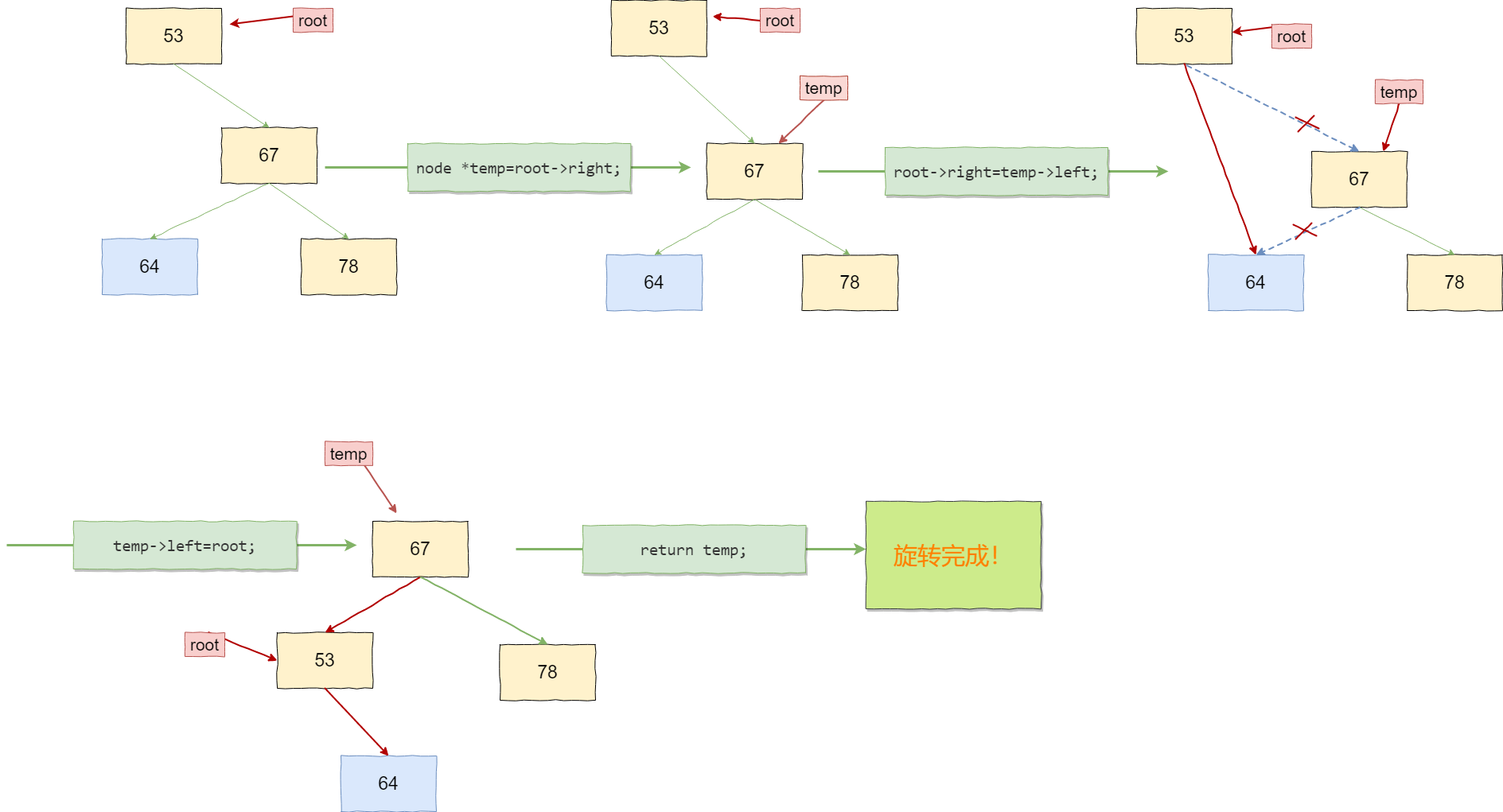 左单旋
左单旋
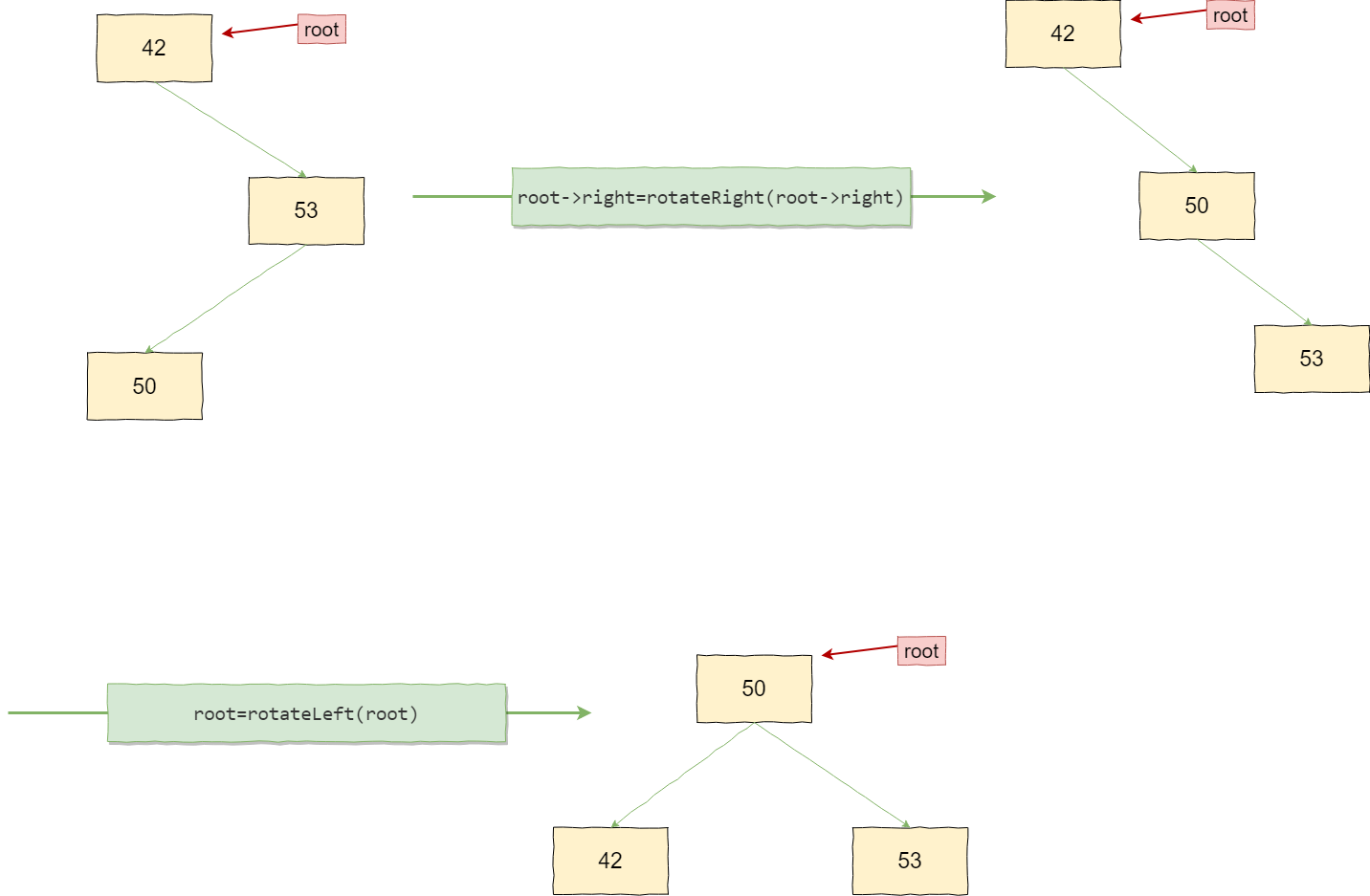 右旋+左旋
右旋+左旋
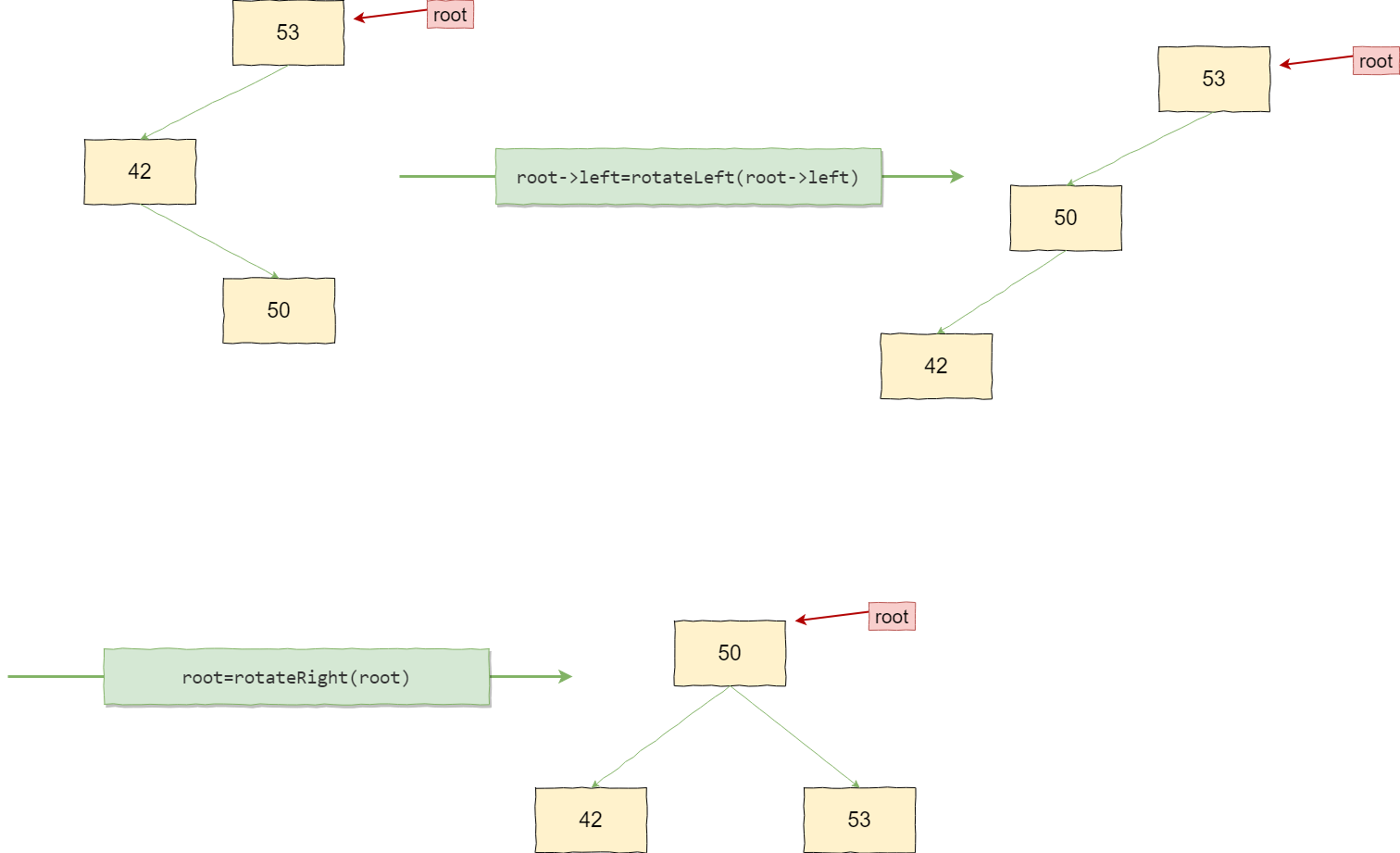 左旋+右旋
左旋+右旋
A1066 Root of AVL Tree (25分)
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print the root of the resulting AVL tree in one line.
Sample Input 1:
5
88 70 61 96 120
Sample Output 1:
70
Sample Input 2:
7
88 70 61 96 120 90 65
Sample Output 2:
88
题目大意,创建一颗平衡二叉树,输出它根节点的值。
#include<bits/stdc++.h>
using namespace std;
struct node{
int val;
node *left,*right;
};
node *rotateRight(node *root){ //右旋
node *temp=root->left;
root->left=temp->right;
temp->right=root;
return temp;
}
node *rotateLeft(node *root){ //左旋
node *temp=root->right;
root->right=temp->left;
temp->left=root;
return temp;
}
node *rotateLR(node *root){ //当失衡的类型为LR,则先左旋再右旋
root->left==rotateLeft(root->left); //先对失衡结点的左结点进行左旋
return rotateRight(root); //再对失衡结点进行右旋
}
node *rotateRL(node *root){ //当失衡的类型为LR,则先右旋再左旋
root->right=(root->right); //先对失衡结点的右结点进行右旋
return rotateLeft(root); //再对失衡结点进行左旋
}
int getHeight(node *root){ //获取树高
if(root==NULL)return 0;
return max(getHeight(root->left),getHeight(root->right))+1;
}
node *insert(node *root,int val){ //插入操作
if(root==NULL){
root=new node;
root->val=val;
root->left=root->right=NULL;
}
else if(val<root->val){
root->left=insert(root->left,val);
if(getHeight(root->left)-getHeight(root->right)==2){
root=val<root->left->val?rotateRight(root):rotateLR(root); //如果新插入的值比该失横结点的左孩子的值小,则是LL型,需要右旋,否则是LR型,需要左旋后右旋
}
}
else{
root->right=insert(root->right,val);
if(getHeight(root->left)-getHeight(root->right)==-2){
root=val>root->val?rotateLeft(root):rotateRL(root); //如果新插入的值比该失衡结点的右孩子的值大,则是RR型,需要左旋,否则是RL型,需要右旋然后左旋
}
}
return root;
}
int main(){
int N,val;
cin>>N;
node *root=NULL;
while(N--){
cin>>val;
root=insert(root,val);
}
cout<<root->val;
return 0;
}
排序建树
给定一个二叉搜索树的先序(后序或者中序)序列,要求还原这个树。
1.根据二叉搜索树的特性可知:二叉搜索树的中序遍历是有序的(从小到大),因此对给定的序列从小到大排序即可得到这颗树的中序遍历。
2.根据先序+中序(后序+中序或者层序+中序)即可还原这二叉搜索树。
#include<bits/stdc++.h>
using namespace std;
struct node {
node *left,*right;
int val;
};
const int maxn=500;
int Pre[maxn],In[maxn];
node *create(int preL,int preR,int InL,int InR){
if(preL>preR)return NULL;
node *root=new node;
root->val=Pre[preL];
int i=InL;
for(i=InL;i<=InR;i++){
if(In[i]==Pre[preL])break;
}
int num=i-InL;
root->left=create(preL+1,preL+num,InL,InL+num-1);
root->right=create(preL+num+1,preR,InL+num+1,InR);
return root;
}
void level(node *root){
queue<node *>q;
q.push(root);
while(!q.empty()){
root=q.front();
q.pop();
cout<<root->val<<' ';
if(root->left!=NULL)q.push(root->left);
if(root->right!=NULL)q.push(root->right);
}
}
int main(){
int N;
cin>>N;
for(int i=0;i<N;i++){
cin>>In[i];
Pre[i]=In[i];
}
sort(In,In+N);
node *root = NULL;
root=create(0,N-1,0,N-1);
level(root);
return 0;
}
最近公共祖先LCA
LCA的在线求法,查询或者结点比较多的情况下时间复杂度会有点高。二叉搜索树跟平衡二叉树求LCA可以直接先序遍历,找到介于u跟v之间的数,即 (u <= lca && lca <= v||v <= lca && lca <= u)
node *LCA(node *root,int u,int v){
if(root==NULL)return NULL;
if(root->val==u||root->val==v) return root;
node *L=LCA(root->left,u,v);
node *R=LCA(root->right,u,v);
if(L!=NULL&&R!=NULL) return root;
return L!=NULL?L:R;
}
